数据结构与算法——堆

1. 什么是堆

堆（Heap），实际上是一种特殊的二叉树，主要知足了二叉树的两个条件：

1. 堆是一种彻底二叉树，还记得彻底二叉树的定义吗？叶节点都在最底下两层，最后一层的节点都靠左排列，而且除了最后一层，其余层的节点个数都要达到最大，这种树叫作彻底二叉树。
2. 堆中的每一个节点的值都必须大于等于（或者小于等于）其左右子节点的值。

对于堆中的每一个节点都大于等于其左右子节点的值，叫作大顶堆，反之，则叫作小顶堆。看看下面的图就能懂了。

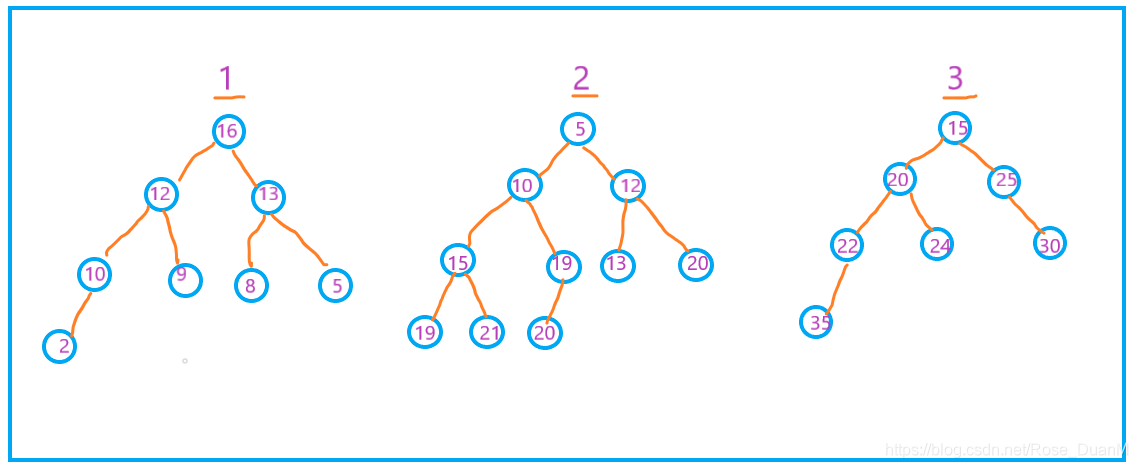
其中，1 是大顶堆，2 是小顶堆，3 不是堆。

2. 堆是如何存储的？

其实，堆能够按照彻底二叉树的存储方式来储存，由于彻底二叉树是比较省空间的，因此咱们能够直接用数组来存储，而后按照数组下标来取出堆中数据。参照下图，来看看堆的存储：

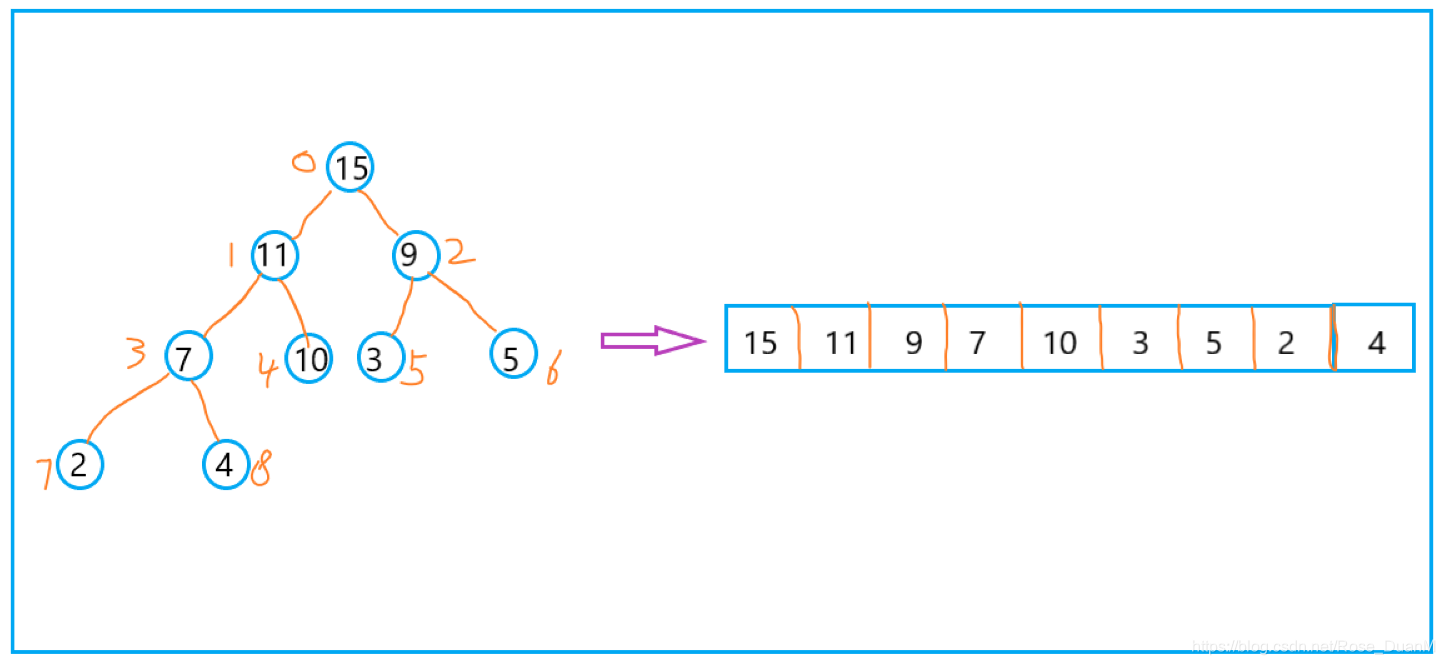
其中，对于任意位置上的节点 i ，其左子节点是 2 * i + 1，右子节点是 2 * i + 2，父节点是 (i - 1) / 2。

3. 堆的几种操做

明白了堆是怎样储存的，咱们在来看看堆最多见的两个操做：往堆中插入元素和删除堆顶元素。

首先，若是要往堆中插入一个元素，咱们先将其插入到数组中最后一个位置，而后与其父节点的值进行比较，若是大于父节点，则交换位置，继续比较。看看下面的图你就明白了：

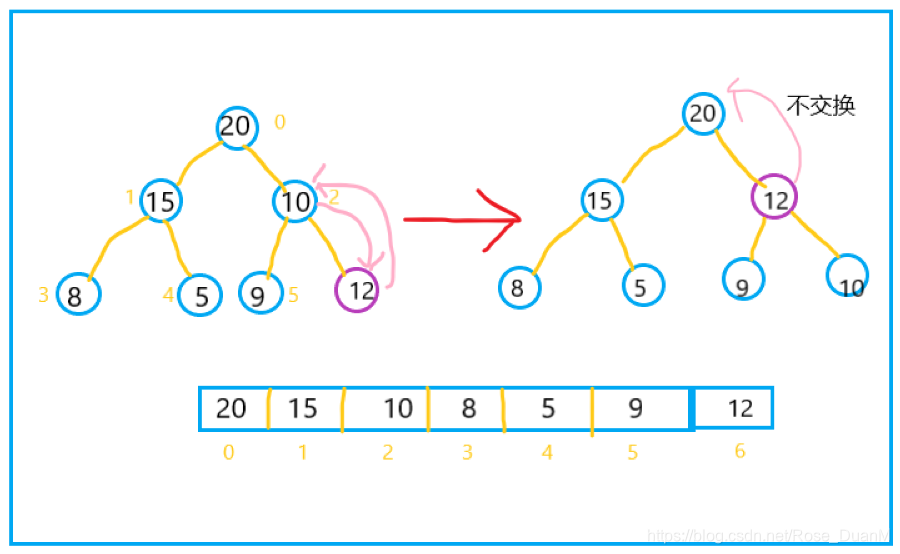
交换操做的代码，我也放到这里：

public class Heap {
    private int[] data;//存储堆数据的数组
    private int n;//堆中可存储的元素容量
    private int size;//堆中存储的元素个数

    public Heap(int capacity) {
        this.data = new int[capacity];
        this.n = capacity;
        this.size = 0;
    }

    //往堆中插入数据
    public void insert(int value){
        if (size >= n) return;//堆满了
        data[size] = value;
        int i = size;

        while ((i - 1) / 2 >= 0 && data[i] > data[(i - 1) / 2]){
            //交换data[i] 极其父节点 data[(i - 1) / 2] 的值
            swap(data, i, (i - 1) / 2);
            i = (i - 1) / 2;
        }
        size ++;
    }
    
    //交换数组两个位置的元素
    private void swap(int[] data, int i, int j){
        int temp = data[i];
        data[i] = data[j];
        data[j] = temp;
    }
}

接下来看看第二种操做：删除堆顶元素。

根据堆的定义，堆顶元素其实就是堆的最大或最小元素。因此删除堆顶元素，咱们只须要移除数组中的第 0 个元素，而后再进行堆化，让堆继续保持顺序。那该怎么进行堆化呢？

首先咱们直接将堆中的最后一个元素移到堆顶，而后与其左右子节点的值进行比较，找到较大的那么子节点，交换位置，而后继续比较，你能够结合代码来理解一下：

//删除数据，若是是大顶堆，则删除的是堆中的最大元素
    //若是是小顶堆，则删除的堆中的最小元素
    public int removeMax(){
        if (size == 0) return -1;//堆为空
        //将数组中的最后一个元素，放到第一个位置
        int result = data[0];
        data[0] = data[size - 1];
        data[-- this.size] = 0;
        //进行堆化
        heapify(data, size, 0);
        return result;
    }
    
    //堆化函数
    private void heapify(int[] data, int size, int i){
        while (true){
            int max = i;
            if ((2 * i + 1) < size && data[i] < data[2 * i + 1]) max = 2 * i + 1;
            if ((2 * i + 2) < size && data[max] < data[2 * i + 2]) max = 2 * i + 2;
            if (max == i) break;
            swap(data, i, max);
            i = max;
        }
    }

4. 堆排序

如今来看看里用堆这种数据结构是怎么实现排序功能的。堆排序的时间复杂度很是的稳定，是O(nlogn)，而且是原地排序算法，具体是怎么实现的呢？咱们通常把堆排序分为两个步骤：建堆和排序。

建堆
对于一个未排序的数组，例如 data[3,5,8,2,1,4,6]，其原始的结构是这样的：

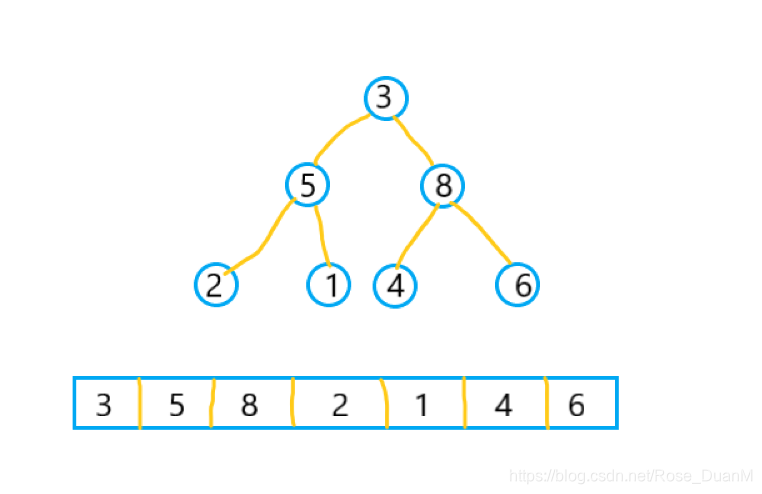
能够看到第一个非叶子节点是 8，因此咱们从 8 开始从上往下堆化，而后依次是 5 - 3，堆化后的效果就是这样的：

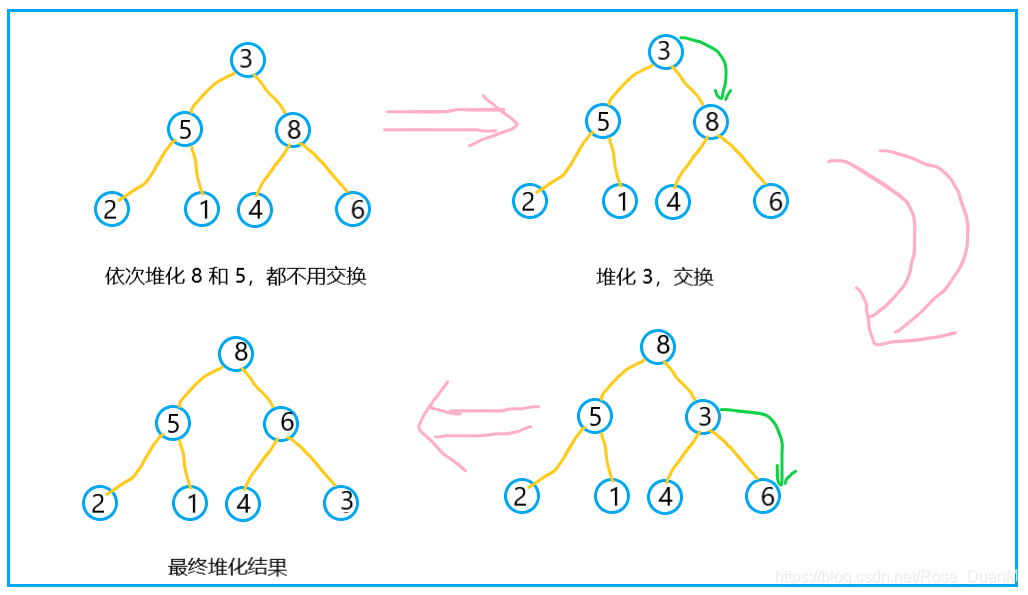
这样，咱们就将一个无序的数组堆化成了具备堆的性质的数据，还须要说明如下，若是肯定一个堆的第一个非叶子节点是多少呢？实际上，对于长度为 length 的数组，(length - 2) / 2下标对应的数据，就是堆中的第一个非叶子节点。接下来的操做就是排序了。

排序
排序的过程相似于上面说到的删除堆顶元素，由于堆顶元素是堆的最大或最小元素，以大顶堆为例，咱们只须要将堆顶元素和数组中最后一个元素交换位置，而后从新构造堆，继续交换堆顶元素和数组中最后一个未排序数据，知道堆中元素剩下最后一个。

示意图以下：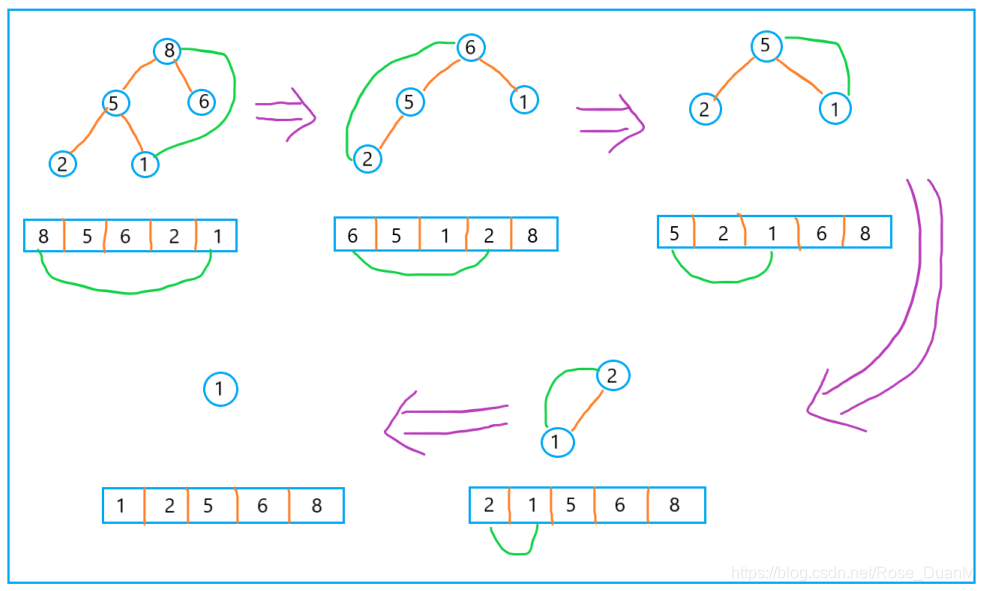

整个建堆和排序的实现的代码也贴在这里：

//堆排序
    public void heapSort(int[] data){
        int length = data.length;
        if (length <= 1) return;
        //建堆
        buildHeap(data);

        while (length > 0){
            swap(data, 0, --length);
            heapify(data, length, 0);
        }
    }
    //建堆
    //从非叶子节点依次堆化
    private void buildHeap(int[] data){
        int length = data.length;
        for (int i = (length - 2) / 2; i >= 0; -- i) {
            heapify(data, length, i);
        }
    }