趣味集算：八皇后问题

有关国际象棋的问题不少，八皇后问题就是其中至关著名的一个。在 8×8 的国际象棋棋盘中，放入 8 个皇后，使它们不互相攻击，共有多少种方法呢？

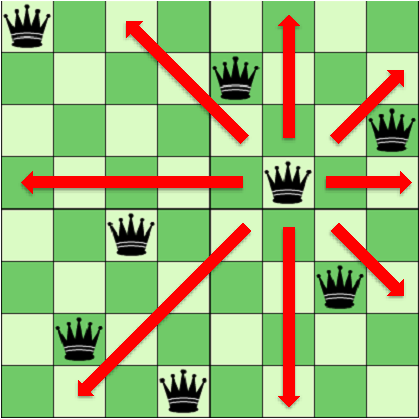
国际象棋中皇后的威力巨大，攻击范围是同一行、同一列以及同一斜行，所以，符合条件的 8 个皇后必须都不在同一行、同一列或者同一斜行上。

因为每一行中只能放入一个皇后，因此可使用一个长度为 8 的序列，依次设入每行中皇后所在的列数，以此来表示皇后的放置状态。当某一行尚未置入皇后时，即该行没有一列上有皇后，记为 0；而每次置入新的皇后时，若是列数不是序列中已有的，就说明没有皇后在同一列中。这样，不一样行、不一样列就能很容易的断定了。

那么，在置入新的皇后时，就只须要保证它与已有的皇后都不在同一斜行上了。若是一个皇后在 m 行 k 列，那么在 m+n 行，最多只有两个位置和它在同一斜行上，并且这两个位置距离它的横向距离等于纵向距离，也就是说最多

只有 (m+n,k+n) 和 (m+n,k-n) 这两个位置与这个皇后在同一斜行上。

这样，只要把每一个皇后在每一行的全部状况都检查一遍，就能够知道共有多少种状况知足要求了。

---

通过上面的抽象分析，咱们只须要在集算器中，经过循环计算来完成这些判断就好了。具体代码以下：

第 1 行，A1 就是记录皇后放置状态的序列；B1 定义了一个变量 i，用来在计算时记录当前放置皇后的行。

第 2 行代码，每循环一次，就把当前行的皇后下移 1 列，用这样的方法遍历行中每一个位置。

第 3 行代码，若是棋子移到了第 9 列，说明当前行的棋子已经完成了全部位置的循环，此时，应该把当前行的记录复原为 0，并将 i 减 1，能够返回去继续上一行的遍历；特别的，当第 1 行也所有循环后，说明完成了遍历，此时 i 被设为 0，中止循环。

第 4 行代码，在移动第 1 行皇后时，能够不用判断，直接开始放置第 2 个皇后。

第 6 行代码，判断已放好的皇后中，是否存在同一列的；

第 7 行代码，判断已放好的皇后中，是否存在同一斜行的。若是既没有同一列的，也没有同一斜行的，就能够继续放置下一行的皇后了。

若是此时 8 个皇后都放置成功，则在第 9 行代码中记录下当前每一个皇后的位置。

通过计算，A10 中结果以下：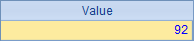

能够在 C1 中查看具体结果：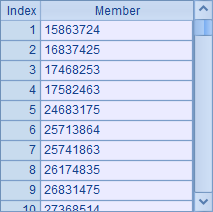

---

固然，还能够用经典的递归方式解决这个问题，集算器中递归调用子函数的方法的代码以下：

在 A2 定义的子程序中，在一个新行中尝试放置皇后，在 B2 中循环每个可能的列。

A5 中的子程序用来判断新的一行是否可使用指定的列，其中在 C5 中查看是否本列已存在皇后，第 6 行查看是否已有皇后在同一斜行，在这样的状况下说明不能放置。若是某一列能够放置，则判断是否 8 个皇后都放置成功，若是已所有设置成功则记录在 C1 中。若是未放置满，则递归调用 A2 中的子程序，继续在下一行放置。这种方法的代码更易理解，计算结果与前面的方法是相同的。