100天搞定机器学习|Day60 遇事不决，XGBoost

XGBoost 是一种集大成的机器学习算法，可用于回归，分类和排序等各类问题，在机器学习大赛及工业领域被普遍应用。成功案例包括：网页文本分类、顾客行为预测、情感挖掘、广告点击率预测、恶意软件分类、物品分类、风险评估、大规模在线课程退学率预测。

XGBoost是初学者最值得深度理解的模型之一，它将决策树、boosting、GBDT 等知识点串联起来，强烈建议你们都手撸一波。
本文我将从XGBoost渊源及优势、模型原理及优化推导、XGBoost模型参数解析、调参实例，XGBoost可视化等方面介绍XGBoost。提醒一下，XGBoost 是在 GBDT 基础上的改进，阅读本文需对 GBDT 有必定的了解，不熟悉的同窗能够看一下前篇： 100天搞定机器学习|Day58 机器学习入门：硬核拆解GBDT

XGBoost渊源及优点

在数据建模中，常常采用Boosting方法，该方法将成百上千个分类准确率较低的树模型组合起来，成为一个准确率很高的预测模型。这个模型会不断地迭代，每次迭代就生成一颗新的树。但在数据集较复杂的时候，可能须要几千次迭代运算，这将形成巨大的计算瓶颈。

针对这个问题，华盛顿大学的陈天奇博士开发的XGBoost（eXtreme Gradient Boosting）基于C++经过多线程实现了回归树的并行构建，并在原有Gradient Boosting算法基础上加以改进，从而极大地提高了模型训练速度和预测精度。

XGBoost 主要优点以下：

一、GBDT在优化时只用到一阶导数信息，XGBoost同时用到了一阶和二阶导数，还支持自定义损失函数，前提是损失函数可一阶和二阶求导；

二、加入了正则项，用于控制模型的复杂度，防止过拟合；

三、借鉴了随机森林的作法，支持列抽样(随机选择特征)，不只能下降过拟合，还能减小计算；

四、寻找最佳分割点时，实现了一种近似法，还考虑了稀疏数据集、缺失值的处理，大大提高算法的效率；

五、支持并行；

六、近似直方图算法，用于高效地生成候选的分割点；

七、在算法实现时作了不少优化，大大提高了算法的效率，内存空间不够时，利用了分块、预取、压缩、多线程协做的思想。

XGBoost模型原理及优化推导

XGBoost其实也是GBDT的一种，仍是加性模型和前向优化算法。

加法模型就是说强分类器由一系列弱分类器线性相加而成。通常组合形式以下：
$$F_M(x;P)=\sum_{m=1}^n\beta_mh(x;a_m)$$
其中，$h(x;a_m)$就是一个个的弱分类器，$a_m$是弱分类器学习到的最优参数，$β_m$就是弱学习在强分类器中所占比重，P是全部$α_m$和$β_m$的组合。这些弱分类器线性相加组成强分类器。

前向分步就是说在训练过程当中，下一轮迭代产生的分类器是在上一轮的基础上训练得来的。也就是能够写成这样的形式：
$$F_m (x)=F_{m-1}(x)+ \beta_mh_m (x;a_m)$$

XGBoost 的模型是什么样子的呢？

$$\hat{y}i = \sum{k=1}^K f_k(x_i), f_k \in \mathcal{F}$$

• 其中 K 是树的棵数。
• $f$是回归树，$f(x)=w_{q(x)}$，知足$(q: R^m \rightarrow T, w \in R^T)$
• q表示每棵树的结构，它会将一个训练样本实例映射到相对应的叶子索引上。
• T是树中的叶子数。
• 每一个对应于一个独立的树结构q和叶子权重w。
• $\mathcal{F}$ 是全部回归树组成的函数空间。

与决策树不一样的是，每棵回归树包含了在每一个叶子上的一个连续分值，咱们使用来表示第i个叶子上的分值。对于一个给定样本实例，咱们会使用树上的决策规则(由q给定)来将它分类到叶子上，并经过将相应叶子上的分值(由w给定)作求和，计算最终的预测值。

XGBoost的学习

为了在该模型中学到这些函数集合，咱们会对下面的正则化目标函数作最小化：

$$\text{obj}(\theta) = \sum_i^n l(y_i, \hat{y}i) + \sum{k=1}^K \Omega(f_k)$$

其中：$l$ 是损失函数，常见的有 2 种：
平方损失函数：$l(yi,y^i)=(y_i−yi)2$
逻辑回归损失函数：$l(yi,y^{i)=y_i\ln\left(1+e}{-\hat{y}_i}\right)+\left(1-y_i\right)\ln\left(1+e^{\hat{y}_i}\right)$

$Ω(Θ)$: 正则化项，用于惩罚复杂模型，避免模型过度拟合训练数据。经常使用的正则有L1正则与L2正则:
L1正则（lasso）: $Ω ( w ) = λ∣∣w∣∣_1$
L2正则: $Ω ( w ) = \lambda ||w||^2$

下一步就是对目标函数进行学习，每一次保留原来的模型不变，加入一个新的函数$f$到咱们的模型中。
$$\begin{split}\hat{y}_i^{(0)} &= 0\
\hat{y}_i^{(1)} &= f_1(x_i) = \hat{y}_i^{(0)} + f_1(x_i)\
\hat{y}_i^{(2)} &= f_1(x_i) + f_2(x_i)= \hat{y}i^{(1)} + f_2(x_i)\
&\dots\
\hat{y}i^{(t)} &= \sum{k=1}^t f_k(x_i)= \hat{y}i^{(t-1)} + f_t(x_i)\end{split}$$
其中，$\hat{y_i}^{(t)}$为第i个实例在第t次迭代时的预测，咱们须要添加树 $f_t$，而后最小化下面的目标函数：
$$
\begin{split}\text{obj}^{(t)} & = \sum{i=1}^n l(y_i, \hat{y}i^{(t)}) + \sum{i=1}^t\Omega(f_i) \
& = \sum{i=1}^n l(y_i, \hat{y}_i^{(t-1)} + f_t(x_i)) + \Omega(f_t) + \mathrm{constant}\end{split}
$$
假设损失函数使用的是平方损失$l(yi,y^i)=(y_i−yi)2$ ，则上式进一步写为：

$$
\begin{split}\text{obj}^{(t)} & = \sum_{i=1}^n (y_i - (\hat{y}i^{(t-1)} + f_t(x_i)))^2 + \sum{i=1}^t\Omega(f_i) \
& = \sum_{i=1}^n [2(\hat{y}_i^{(t-1)} - y_i)f_t(x_i) + f_t(x_i)^2] + \Omega(f_t) + \mathrm{constant}\end{split}
$$

如今，咱们采用泰勒展开来定义一个近似的目标函数：

$\text{obj}^{(t)} = \sum_{i=1}^n [l(y_i, \hat{y}_i^{(t-1)}) + g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t) + \mathrm{constant}$

其中：
$$\begin{split}g_i &= \partial_{\hat{y}_i^{(t-1)}} l(y_i, \hat{y}i^{(t-1)})\
h_i &= \partial{\hat{y}_i^{(t-1)}}2 l(y_i, \hat{y}_i^{(t-1)})\end{split}$$
$g_i,h_i$分别是loss function上的一阶梯度和二阶梯度。

忘记基础知识的同窗顺便重温一下泰勒公式吧

泰勒公式（Taylor’s Formula）是一个用函数在某点的信息描述其附近取值的公式。其初衷是用多项式来近似表示函数在某点周围的状况。

函数$f(x)$在$x_0$处的基本形式以下
$$
\begin{align}
f(x) &= \sum_{n=0}^{\infty\frac{f}{(n)}(x_0)}{n!}(x-x_0)^n
\&= f(x_0) +f^{1}(x_0)(x-x_0)+ \frac{f^{{2}(x_0)}{2}(x-x_0)}2 + \cdots + \frac{f^{{(n)}(x_0)}{n!}(x-x_0)}n
\end{align}
$$
还有另一种常见的写法，$x^{t+1} = x^t + \Delta x$,将$f(x^{t+1})$在$xt$处进行泰勒展开，得：
$$\begin{align}
f(x^{t+1}) &= f(x^t) +f^{1}(xt)\Delta x+ \frac{f^{2}(xt)}{2}\Delta x^2 + \cdots
\end{align}$$

如今，咱们去掉常量，而后从新认识一下咱们新的目标函数：

$$\sum_{i=1}^n [g_i f_t(x_i) + \frac{1}{2} h_i f_t^2(x_i)] + \Omega(f_t)$$

定义$I_j = {i|q(x_i)=j}$是叶子 j 的实例集合。
$\Omega(f) = \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2$
将正则项带入，展开目标函数：
$$
\begin{split}\text{obj}^{(t)} &\approx \sum_{i=1}^n [g_i w_{q(x_i)} + \frac{1}{2} h_i w_{q(x_i)}^2] + \gamma T + \frac{1}{2}\lambda \sum_{j=1}^T w_j^2\
&= \sum^T_{j=1} [(\sum_{i\in I_j} g_i) w_j + \frac{1}{2} (\sum_{i\in I_j} h_i + \lambda) w_j^2 ] + \gamma T\end{split}$$

看起来有点复杂，令：
$G_j = \sum_{i\in I_j} g_i$，$H_j = \sum_{i\in I_j} h_i$，上式简化为：
$$
\text{obj}^{(t)} = \sum^T_{j=1} [G_jw_j + \frac{1}{2} (H_j+\lambda) w_j^2] +\gamma T
$$
上式中$w_j$是相互独立的，$G_jw_j+\frac{1}{2}(H_j+\lambda)w_j^2$是平方项。
对于一个肯定的结构$q(x)$，咱们能够计算最优的权重$w_j^{\ast}$:

$$
\begin{split}w_j^\ast &= -\frac{G_j}{H_j+\lambda}\
\end{split}
$$

将$w_j^{{\ast}$带入上式，计算获得的loss最优解${obj}}*$：

$$\begin{align}
Obj^{\ (t)} &=\sum_{j=1}^T \left(G_jw_j + \frac{1}{2} (H_j + \lambda) w_j^2\right) +\gamma T\
&=\sum_{j=1}^T \left(- \frac{G_j^2}{H_j+\lambda} + \frac{1}{2} \frac{G_j^2}{H_j+\lambda} \right) +\gamma T\
&=- \frac{1}{2}\sum_{j=1}^T \left({\color{red}{\frac{G_j^2}{H_j+\lambda}} } \right) +\gamma T \tag{2-8}
\end{align}$$

${obj}^*$能够做为一个得分函数（scoring function）来衡量一棵树结构$q(x)$的质量。

咱们有了一个方法来衡量一棵树有多好，如今来看XGBoost优化的第二个问题：如何选择哪一个特征和特征值进行分裂，使最终咱们的损失函数最小？

XGBoost特征选择和切分点选择指标定义为：
$$
\begin{align}
gain=\underbrace{\frac{G_L^{2}{H_L+\lambda}}_{左节点得分}+\underbrace{\frac{G_R}2}{H_R+\lambda}}{右节点得分}-\underbrace{\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}}{切分前得分}-\gamma
\end{align}
$$

具体如何分裂？

可使用彻底贪婪算法(exact greedy algorithm)，在全部特征上，枚举全部可能的划分。

• 基于当前节点尝试分裂决策树，默认分数score=0，G和H为当前须要分裂的节点的一阶二阶导数之和。
• 对特征序号 k=1,2...K:$G_L=0, H_L=0$
• 将样本按特征k从小到大排列，依次取出第i个样本，依次计算当前样本放入左子树后，左右子树一阶和二阶导数和：
  $G_L = G_L+ g_{ti}, G_R=G-G_L$
  $H_L = H_L+ h_{ti}, H_R=H-H_L$
• 尝试更新最大的分数：
  $$score = max(score, \frac{1}{2}\frac{G_L^2}{H_L + \lambda} + \frac{1}{2}\frac{G_R^2}{H_R+\lambda} - \frac{1}{2}\frac{(G_L+G_R)^2}{H_L+H_R+ \lambda} -\gamma)$$
• 基于最大score对应的划分特征和特征值分裂子树。
• 若是最大score为0，则当前决策树创建完毕，计算全部叶子区域的$w_{tj}$, 获得弱学习器$h_t(x)$，更新强学习器$f_t(x)$,进入下一轮弱学习器迭代.若是最大score不是0，则继续尝试分裂决策树。

原理推导（精简版）

下面是XGBoost原理推导的精简版，方便同窗们复习使用。
$$
\begin{align*}
\begin{array}{l}
\text{预测模型: }F(x)=\sum_{i=1}^Tw_if_i(x)\
\text{目标函数: }obj^t=\sum_{i=1}NL(y_i,F_i^t(x_i))+\Omega(f_t)\

\because obj^t=\sum_{i=1}^NL(y_i,F_i^t(x_i))+\Omega(f_t)\\
~~~~~~~~~=\sum_{i=1}^NL(y_i,F_i^{t-1}(x_i)+w_tf_t(x_i))+\Omega(f_t)\\
\text{由泰勒公式: }f(x+\Delta x)\thickapprox f(x)+\nabla f(x)\Delta x+\frac{1}{2}\nabla^2 f(x)\Delta x^2\\
\therefore obj^t\thickapprox\sum_{i=1}^N[L(y_i,F_i^{t-1}(x_i))+\nabla _{F_{t-1}}L(y_i,F_i^{t-1}(x_i))w_tf_t(x_i)\\
~~~~~~~~~~~~~~~\frac{1}{2}\nabla _{F_{t-1}}^2L(y_i,F_i^{t-1}(x_i))w_t^2f_t^2(x_i)]+\Omega(f_t)\\
\text{令 $g_i=\nabla _{F_{t-1}}L(y_i,F_i^{t-1}(x_i))$}\\
~~~~~~h_i=\nabla _{F_{t-1}}^2L(y_i,F_i^{t-1}(x_i))\\
~~~obj^t\thickapprox \sum_{i=1}^N[L(y_i,F_i^{t-1}(x_i))+g_iw_tf_t(x_i)+\frac{1}{2}h_iw_t^2f_t^2(x_i)]+\Omega(f_t)\\
\because L(y_i,F_i^{t-1}(x_i)) \text{ 是常量}\\
\therefore \text{目标函数:}\\
~~~obj^t=\sum_{i=1}^N[g_iw_tf_t(x_i)+\frac{1}{2}h_iw_t^2f_t^2(x_i)]+\Omega(f_t)+C\\
\text{用叶子节点集合以及叶子节点得分表示 ，每一个样本都落在一个叶子节点上:}\\ 
f_t(x)=m_q(x),~~m\in R^T,~~q:R^d\rightarrow\{1,2,3,...,T\}\\
\Omega(f_t)=\gamma T+ \frac{1}{2}\lambda \sum_{i=1}^Tm_j^2,\\
\text{$T$ 是第 $t$ 棵树叶子结点总数}\\
\text{$m_j$ 是第j个叶子结点的权重}\\
\text{定义第 $j$ 个叶子节点所在的样本为 $I_j=\{i|j=q(x_i)\}$}\\
\text{新的目标函数:}\\
obj^t=\sum_{i=1}^N[g_iw_tf_t(x_i)+\frac{1}{2}h_iw_t^2f_t^2(x_i)]+\Omega(f_t)\\
~~~~~~~=\sum_{i=1}^N[g_iw_tm_q(x_i)+\frac{1}{2}h_iw_t^2m_q^2(x_i)]+\gamma T+ \frac{1}{2}\lambda \sum_{i=1}^Tm_j^2\\
~~~~~~~=\sum_{j=1}^T[(\sum_{i \in I_j}g_i)w_tm_j+\frac{1}{2}(\sum_{i \in I_j}h_iw_t^2+\lambda )m_j^2]+\gamma T\\
\text{令： $G_j=\sum_{i \in I_j}g_i$ , $H_j=\sum_{i \in I_j}h_i$ }\\
obj^t=\sum_{j=1}^T[G_jw_tm_j+\frac{1}{2}(H_jw_t^2+\lambda)m_j^2]+\gamma T\\
\text{对二次函数优化问题:}\\
m_j^*=-\frac{G_j^2w_t}{H_jw_t^2+\lambda}\\
obj^*=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2w_t^2}{H_jw_t^2+\lambda}+\gamma T\\
\text{令 $w_t=1$ ：}\\
m_j^*=-\frac{G_j}{H_j+\lambda}\\
obj^*=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2}{H_j+\lambda}+\gamma T\\
\text{因此当咱们新增一个切分点增益为:}\\
gain=\underbrace{\frac{G_L^2}{H_L+\lambda}}_{左节点得分}+\underbrace{\frac{G_R^2}{H_R+\lambda}}_{右节点得分}-\underbrace{\frac{(G_L+G_R)^2}{H_L+H_R+\lambda}}_{切分前得分}-\gamma
\end{array}
\end{align*}
$$


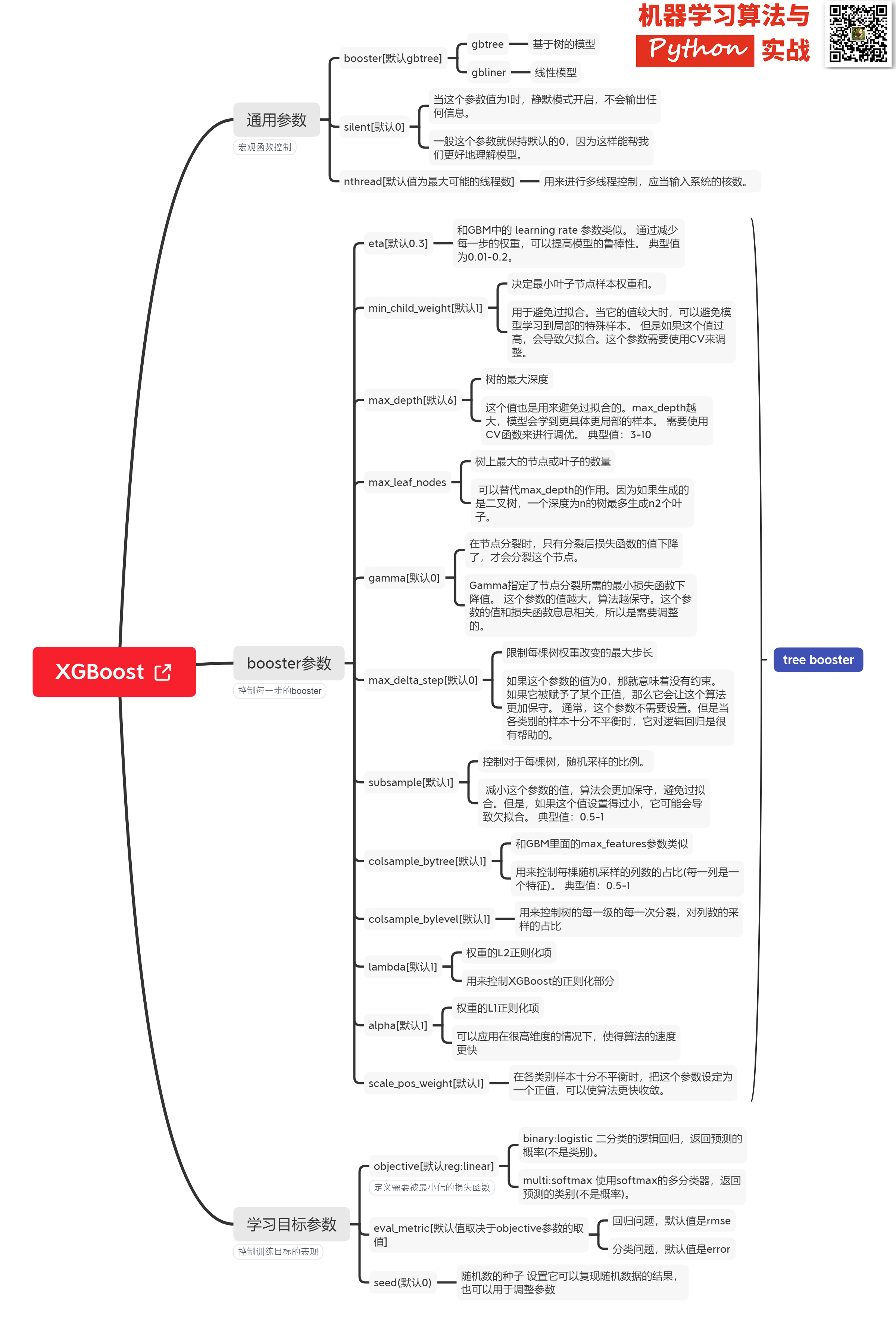
### Xgboost@sklearn模型参数解析
XGBoost的实现有原生版本，同时也有Scikit-learn版本，二者在使用上有一些微差别，这里给出xgboost.sklearn 参数解释。XGBoost使用**key-value**字典的方式存储参数：
```
#部分重要参数
params = {
    'booster': 'gbtree',
    'objective': 'multi:softmax',  # 多分类的问题
    'num_class': 10,               # 类别数，与 multisoftmax 并用
    'gamma': 0.1,                  # 用于控制是否后剪枝的参数,越大越保守，通常0.一、0.2这样子。
    'max_depth': 12,               # 构建树的深度，越大越容易过拟合
    'lambda': 2,                   # 控制模型复杂度的权重值的L2正则化项参数，参数越大，模型越不容易过拟合。
    'subsample': 0.7,              # 随机采样训练样本
    'colsample_bytree': 0.7,       # 生成树时进行的列采样
    'min_child_weight': 3,
    'silent': 1,                   # 设置成1则没有运行信息输出，最好是设置为0.
    'eta': 0.007,                  # 如同窗习率
    'seed': 1000,
    'nthread': 4,                  # cpu 线程数
}
```
![xgboost完整参数解析](https://my-wechat.oss-cn-beijing.aliyuncs.com/XGBoost_20201205091216.png)

篇幅缘由，调参实例及XGBoost可视化且听下回分解。  
若有收获，还请不吝给个**在看、收藏、转发**
## 参考
https://www.cnblogs.com/pinard/p/10979808.html  
https://www.biaodianfu.com/xgboost.html
https://www.zybuluo.com/vivounicorn/note/446479
https://www.cnblogs.com/chenjieyouge/p/12026339.html