疯狂kotlin讲义连载之运算符和表达式——位运算符

时间 2019-12-04

标签疯狂 kotlin 讲义连载运算符表达式繁體版

原文原文链接

3.2 位运算符

Kotlin 虽然也提供了与 Java 功能彻底相同的位运算符，但这些位运算符都不是以特殊字符给出的，而是以infix函数的形式给出的，所以程序只能用函数名来执行这些位运算符。

Kotlin 支持的位运算符一样有以下 7 个。

一、 and(bits) ：按位与。当两位同时为 1 时才返回 1 。

二、 or(bits) ：按位或。只要有一位为 1 便可返回 1 。

三、 inv(bits)：按位非。单目运算符，将操做数的每一个位（包括符号位）所有取反。

四、xor(bits)：按位异或。当两位相同时返回0，不一样时返回1。算法

五、 shl(bits：左移运算符。

六、shr(bits)：右移运算符。函数

七、 ushr(bits)：无符号右移运算符。

Kotlin 位运算符的只能对 Int 或 Long 两种数据类型起做用。位运算符的运算法则如表 3.10 所示。

3.10表

位运算符的运算法则

第一个运算数	第二个运算数	按位与	按位或	按位异或
0	0	0	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	1	0

按位非只须要一个操做数，这个运算符将把操做数在计算机底层的二进制码按位（包括符号位）取反。以下代码测试了按位与和按位或运算的运行结果。

程序清单：

codes\03\3.2\BitOperatorTest.kt
println(5 and 9) // 将输出 1

println(5 or 9) // 将输出 13

程序执行的结果是：

5 and 9 的结果是 1 ， 5 or 9 的结果是 13 。下面介绍运算原理。

5 的二进制码是 00000101 （省略了前面的 24 个 0 ），而 9 的二进制码是 00001001 （省略了前面的 24 个 0 ）。运算过程如图 3.1 所示。

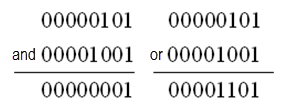
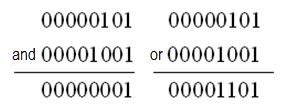
图 3.1 按位与和按位或运算过程

下面是按位异或和按位取反的执行代码（程序清单同上）。
println((-5).inv()) // 将输出 4

println(5 xor 9) // 将输出 12

程序执行 -5按位取反的结果是4，执行5 xor 9的结果是12，下面经过图3.2 来介绍运算原理。

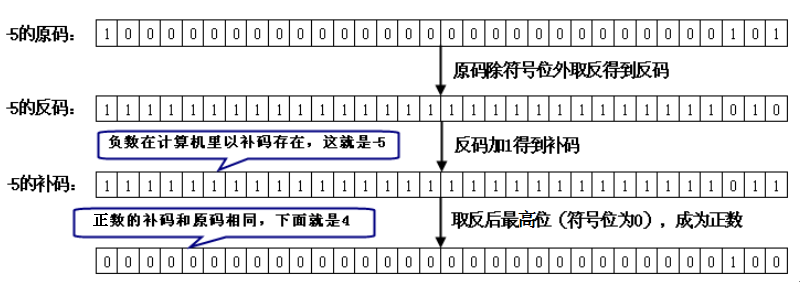
图 3.2 -5 按位取反的运算过程

而 5 xor 9 的运算过程如图 3.3 所示。

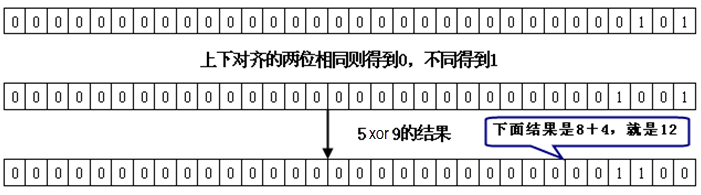
图 3.3 5 xor 9 的运算过程

左移运算符是将运算数的二进制码总体左移指定位数，左移后右边空出来的位以 0 填充。例如以下代码（程序清单同上）：

println(5 shl 2) // 输出 20

println(-5 shl 2) // 输出 -20

下面以-5为例来介绍左移运算的运算过程，如图3.4所示。

图3.4 -5左移两位的运算过程

在图3.4中，上面的32位数是-5的补码，左移两位后获得一个二进制补码，这个二进制补码的最高位是1，代表是一个负数，换算成十进制数就是-20。

Kotlin 的右移运算符有两个：shr 和 ushr ，对于 shr

运算符而言，把第一个操做数的二进制码右移指定位数后，左边空出来的位以原来的符号位填充，即若是第一个操做数原来是正数，则左边补 0 ；若是第一个操做数是负数，则左边补 1 。

ushr 是无符号右移运算符，它把第一个操做数的二进制码右移指定位数后，左边空出来的位老是以 0 填充。

看下面代码（程序清单同上）：

//输出-2post

println(-5 shr 2)测试

//输出1073741822spa

println(-5 ushr 2)3d

下面用示意图来讲明 shr 和 ushr 运算符的运算过程。

从图3.5 来看， -5右移2位后左边空出2位，空出来的2位以符号位补充。从图中能够看出，右移运算后获得的结果的正负与第一个操做数的正负相同。右移后的结果依然是一个负数，这是一个二进制补码，换算成十进制数就是-2。

图3.5-5 右移2 位的运算过程

从图3.6 来看，-5无符号右移2位后左边空出2位，空出来的2位以0补充。从图中能够看出，无符号右移运算后的结果老是获得一个正数。图3.6 中下面的正数是1073741822（230-2）。

图3.6-5 无符号右移2 位的运算过程

进行移位运算时还要遵循以下规则。

一、对于 Int 类型的整数移位 a shr b，当b>32时，系统先用b对32 求余（由于 Int 类型只有 32位），获得的结果才是真正移位的位数。例如，a shr 33和a shr 1的结果彻底同样，而a shr 32的结果和a相同。

二、对于 Long类型的整数移位a shr b，当b>64时，老是先用b对64求余（由于Long类型是64位），获得的结果才是真正移位的位数。

注意：当进行移位运算时，只要被移位的二进制码没有发生有效位的数字丢失（对于正数而言，一般指被移出的位所有都是 0 ），不难发现左移 n 位就至关于乘以 2 的 n 次方，右移 n 位则是除以 2 的 n 次方。不只如此，进行移位运算不会改变操做数自己，只是获得了一个新的运算结果，而原来的操做数自己是不会改变的。

以上内容节选自《疯狂Kotlin讲义》：一本让您最直接认识Kotlin的疯狂讲义code