面经手册 · 第6篇《带着面试题学习红黑树操做原理，解析何时染色、怎么进行旋转、与2-3树有什么关联》

做者：小傅哥
博客：https://bugstack.cn

沉淀、分享、成长，让本身和他人都能有所收获！😄

1、前言

红黑树，是一种高效的自平衡二叉查找树

Rudolf Bayer 于1978年发明红黑树，在当时被称为对称二叉 B 树(symmetric binary B-trees)。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改成现在的红黑树。

红黑树具备良好的效率，它可在近似O(logN) 时间复杂度下完成插入、删除、查找等操做，所以红黑树在业界也被普遍应用，好比 Java 中的 TreeMap，JDK 1.8 中的 HashMap、C++ STL 中的 map 均是基于红黑树结构实现的。

死记硬背，很难学会

红黑树的结构和设计都很是优秀，也一样在实现上有着复杂的处理逻辑，包括插入或者删除节点时；颜色变化、旋转操做等操做。但若是只把这些知识点硬背下来，何时染色、何时旋转，是没有多大意义的，用不了多久也就忘记了。因此这部分的学习，了解其根本更重要。

2、面试题

谢飞机，考你几个红黑树的知识点🦀

1. 红黑树的数据结构都用在哪些场景，有什么好处？
2. 红黑树的时间复杂度是多少？
3. 红黑树中插入新的节点时怎么保持平衡？

🤥飞机，2-3树是不没看，回去等消息吧！

3、2-3树与红黑树的等价性

在上一章节《讲解2-3平衡树「红黑树的前身」》，使用了大量图例讲解了2-3树，并在标题处写出它是红黑树的前身。阅读后更容易理解红黑树相关知识。

红黑树规则

1. 根节点是黑色
2. 节点是红黑或者黑色
3. 全部子叶节点都是黑色(叶子是NIL节点，默认没有画出来)
4. 每一个红色节点必须有两个黑色子节点(也一样说明一条链路上不能有链路的红色节点)
5. 黑高，从任一节点到齐每一个叶子节点，通过的路径都包含相同数目的黑色节点

那么，这些规则是怎么总结定义出来的呢？接下里咱们一步步分析讲解。

1. 为何既有2-3树要有红黑树

首先2-3树(读法：二三树)就是一个节点有1个或者2个元素，而实际上2-3树转红黑树是由概念模型2-3-4树转换而来的。-4叉就是一个节点里有3个元素，这在2-3树中会被调整，可是在概念模型中是会被保留的。

虽然2-3-4树也是具有2-3树一样的平衡树的特性，可是若是直接把这样的模型用代码实现就会很麻烦，且效率不高，这里的复杂点包括；

1. 2-叉、3-叉、4-叉，三种结构的节点类型，互相转换复杂度较高
2. 3-叉、4-叉，节点在数据比较上须要进行屡次，不像2-叉节点，直接布尔类型比较便可非左即右
3. 代码实现上对每种差别，都须要有额外的代码，规则不够标准化

因此，但愿找到一种平衡关系，既保持2-3树平衡和O(logn)的特性，又能在代码实现上更加方便，那么就诞生了红黑树。

2. 简单2-3树转红黑树

2-3树转红黑树，也能够说红黑树是2-3树和2-3-4树的另一种表现形式，也就是更利于编码实现的形式。

简单转换示例；

从上图能够看出，2-3-4树与红黑树的转换关系，包括；

1. 2-叉节点，转换比较简单，只是把原有节点转换为黑色节点
2. 3-叉节点，包括了2个元素，先用红色线把两个节点相连，以后拆分出来，最后调整高度黑色节点在上
3. 4-叉节点，包括了3个元素，分别用红黑线链接，以后拆分出来拉升高度。这个拉升过程和2-3树调整一致，只是添加了颜色

综上，就是2-3-4树的节点转换，总结出来的规则，以下；

1. 将2-3-4树，用二叉树的形式表示
2. 3-叉、4-叉节点，使用红色、黑色连线进行链接
3. 另外，3-叉节点有两种状况，致使转换成二叉树，就有左倾和右倾

3. 复杂2-3树转红黑树

在简单2-3树转换红黑树的过程当中，了解到一个基本的转换规则右旋定义，接下来咱们在一个稍微复杂一点的2-3树与红黑树的对应关系，以下图；

上图是一个稍微复杂点的2-3树，转换为红黑树的过程，是不这样一张图让你对红黑树更有感受了，同时它也知足一下条件；

1. 从任意节点到叶子节点，所通过的黑色节点数目相同
2. 黑色节点保持着总体的平衡性，也就是让整个红黑树接近于O(logn)时间复杂度
3. 其余红黑树的特色也都知足，能够对照红黑树的特性进行比对

4、红黑树

1. 平衡操做

经过在上一章节2-3树的学习，在插入节点时并不会插到空位置，而是与现有节点融合以及调整，保持整个树的平衡。

而红黑树是2-3-4树的一种概念模型转换而来，在插入节点时经过红色连接相连，也就是插入红色节点。插入完成后进行调整，以保持树接近平衡。

那么，为了让红黑树达到平衡状态，主要包括染色、↔左右旋转、这些作法其实都是从2-3树演化过来的。接下来咱们就分别讲解几种规则的演化过程，以此更好了解红黑树的平衡操做。

1.1 左旋转

左旋定义： 把一个向右倾斜的红节点连接(2-3树，3-叉双元素节点)，转化为左连接。

背景：顺序插入元素，一、二、3，2-3树保持平衡，红黑树暂时处于右倾斜。

接下来咱们分别对比两种树结构的平衡操做；

1. 2-3树，全部插入的节点都会保持在一个节点上，以后经过调整节点位置，保持平衡。
2. 红黑树，则须要经过节点的左侧旋转，将元素2拉起来，元素1和元素3，分别成为左右子节点。

红黑树的左旋，只会处理与之对应的2-3树节点进行操做，不会总体改变。

1.2 右旋转

右旋定义： 把一个向左倾斜的红节点链接(2-3树，3-叉双元素节点)，转换为右链接。

背景：顺序插入元素，三、一、1，2-3树保持平衡，红黑树暂时处于左倾斜。

接下来咱们分别对比两种树结构的平衡操做；

1. 2-3树，全部插入的节点都会保持在一个节点上，以后经过调整节点位置，保持平衡。
2. 红黑树，则须要经过节点的右侧旋转，将元素2拉起来，元素1和元素3，分别成为左右子节点。

你会发现，左旋与右旋是相互对应的，但在2-3树中是保持不变的

1.3 左右旋综合运用

左旋、右旋，咱们已经有了一个基本的概念，那么接下来咱们再看一个能够综合左右旋以及对应2-3树的演化案例，以下；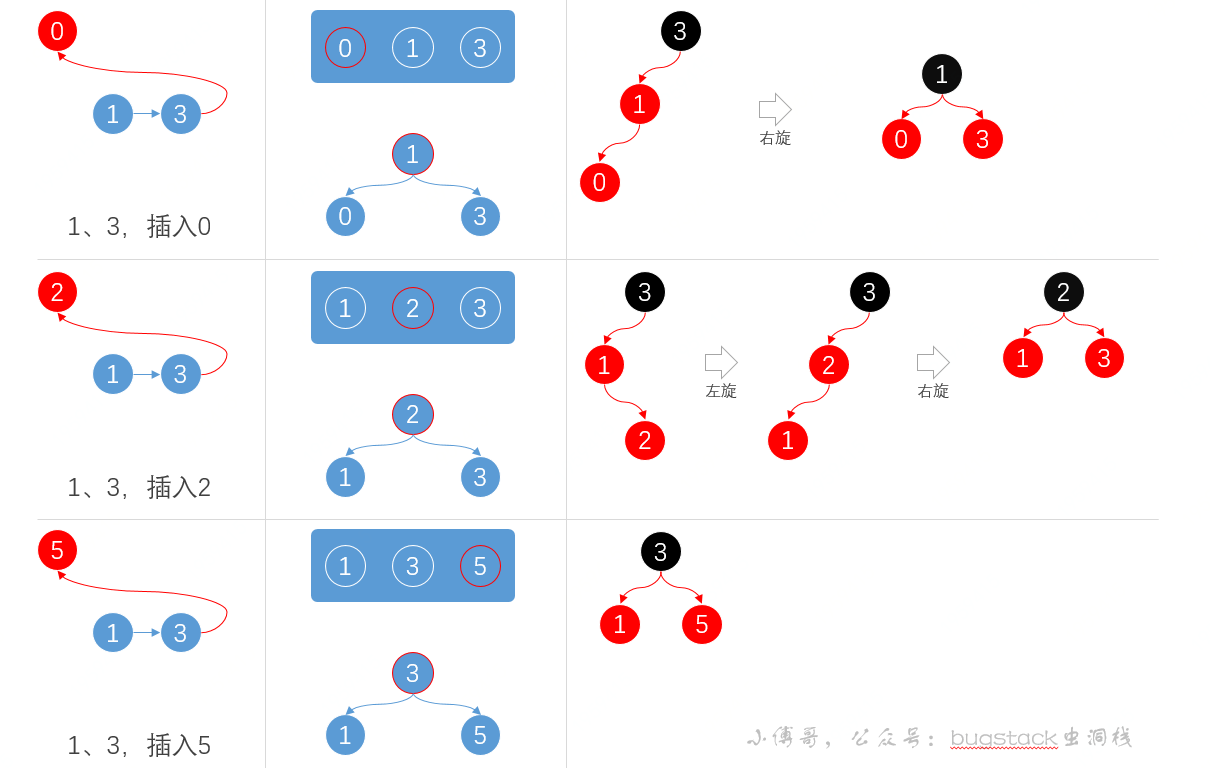

以上的例子分别演示了一个元素插入的三种状况，以下；

1. 一、3，插入0，左侧底部插入，与2-3树相比，须要右旋保持平衡
2. 一、3，插入2，中间位置插入，首先进行左旋调整元素位置，以后进行右旋进行树平衡
3. 一、3，插入5，右侧位置插入，此时正好保持树平衡，不须要调整

1.4 染色

在2-3树中，插入一个节点，为了保持树平衡是不插入到空位置上的，当插入节点后元素数量有3个后则须要调整中间元素向上，来保持树平衡。与之对应的红黑树则须要调整颜色，来保证红黑树的平衡规则，具体参考以下；

2. 旋转+染色运用案例

接下来咱们把上面讲解到的旋转、染色，运用到一个实际案例中，以下图；

• 首先从左侧开始，是一个按照顺序插入生产出来的红黑树，插入顺序；`七、二、八、一、四、三、5

`

• α，向目前红黑树插入元素6，插入后右下角有三个红色节点；三、五、6。
• β，由于右下角知足染色条件，变换后；黑色节点(三、5)、红色节点(四、6)。
• γ，以后看被红色连线连接的节点七、四、2，最小节点在中间，左旋平衡树结构。
• δ，左旋完成后，红色连接线的七、四、2为作倾顺序节点，所以须要作右旋操做。
• ε，左旋、右旋，调整完成后，又知足了染色操做。到此恢复红黑树平衡。

注意，全部链接红色节点的，都是是红色线。以此与2-3树作对应。

3. 删除操做

根据2-3-4树模型的红黑树，在删除的时候基本是按照2-3方式进行删除，只不过在这个过程当中须要染色和旋转操做，以保持树平衡。删除过程主要能够分为如图四种状况，以下；

3.1 删除子叶红色节点

红色子叶节点的删除并不会破坏树平衡，也不影响树高，因此直接删除便可，以下；

3.2 删除左侧节点

3.2.1 被删节点兄弟为黑色&含右子节点

3.2.2 被删节点兄弟为黑色&含左子节点

3.2.3 被删节点兄弟为黑色&含双子节点(红)

3.2.4 被删节点兄弟为黑色&不含子节点

3.2.5 被删节点兄弟为黑色&含双黑节点(黑)

3.3. 删除右侧节点

3.3.1 被删节点兄弟为黑色&含左子节点

3.3.2 被删节点兄弟为黑色&含右子节点

3.3.3 被删节点兄弟为黑色&含双子节点(红)

3.2.4 被删节点兄弟为黑色&不含子节点

3.2.5 被删节点兄弟为黑色&含双黑节点(黑)

5、总结

• 从2-3树到解释2-3-4树概念推导出红黑树，从元素的在2-3树中的插入删除对照到红黑树中保持平衡操做，从原理解析到各项状况实际操做等，以及把绝大部分成黑树内容所有介绍完成。
• 红黑树的原理理解要比背概念更重要，这是一种数据结构的学习，更重要的是技术迁移学习，而不是为了面试背几道题。可能这个学习过程很是烧脑，但适合学习根本。

• 在编写本篇文章时，参考了大量的资料进行校订，包括优秀文章；

  • 红黑树可视化：https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
  • 左倾红黑树论文： Left-leaning Red-Black Trees

6、系列推荐

• 面试官都问我啥
• HashMap核心知识，扰动函数、负载因子、扩容链表拆分，深度学习
• HashMap数据插入、查找、删除、遍历，源码分析
• 重学 Java 设计模式，内功心法修炼，22个互联网真实业务场景实战
• DDD领域驱动设计实践，领域层决策规则树服务设计