从“数学概括法”到理解“递归算法”！

每章一点正能量：人的一辈子可能燃烧也可能腐朽。

前言

相信你们在面试或者工做中偶尔会遇到递归算法的提问或者编程，咱们今天来聊一聊从数学概括法到理解递归算法。若有错误还请你们及时指出~

本文已同步至 GitHub/ Gitee/公众号，感兴趣的同窗帮忙点波关注~

1. 数学概括法

1.1 简介

来源百度百科

数学概括法（Mathematical Induction, MI）是一种数学证实方法，一般被用于证实某个给定命题在整个（或者局部）天然数范围内成立。除了天然数之外，广义上的数学概括法也能够用于证实通常良基结构，例如：集合论中的树。这种广义的数学概括法应用于数学逻辑和计算机科学领域，称做结构概括法。在数论中，数学概括法是以一种不一样的方式来证实任意一个给定的情形都是正确的（第一个,第二个，第三个，一直下去概不例外）的数学定理。虽然数学概括法名字中有“概括”，可是数学概括法并不是不严谨的概括推理法，它属于彻底严谨的演绎推理法。事实上，全部数学证实都是演绎法。

天然数是指表示物体个数的数，即由0开始，0，1，2，3，4，……一个接一个，组成一个无穷的集体，即指非负整数。

1.2 推演步骤

简单了解数学概括法的概念后，咱们来看看数学概括法的推演步骤。

咱们知道数学概括法用来证实任意一个给定的情形都是正确的，也就是说，第一个，第二个，一直到全部情形，概不例外。

其证实步骤以下：

1. 证实基本状况（一般是N = 1 的时候）是否成立。

证实对于N=1成立。咱们只须要先从最小的天然数开始证实。这一步一般很是简单。关键是证实第二步。

1. 证实N > 1 时，假设 N - 1 成立，那么对于N成立（N为任意大于1的天然数）。

这一步并非直接证实的，而是假设N-1成立，利用这个结论推出N是成立的。若是可以推出的话，就能够说：对于全部的天然数都成立。由于证实了对1成立，那么对2成立，对3也成立。那么就证实了对全部天然数都成立。
咱们会发现数学概括法它很合适用来证实，例如常见的等差、等比、以及平方、立方数列的求和等等。

1.3 小栗子

咱们来举一个小栗子，回顾下咱们高中时期所学的数学概括法是如何进行证实。

例子：

证实： 1+2+3+...+n = n(n+1)/2

咱们来将上面 1.2 推演步骤 用起来。

• 第一步： 证实基本状况（一般是N = 1 的时候）是否成立。

咱们把N=1同时代入等号左边和右边，得

1 = 1*(1+1)/2

成立！

• 第二步： 证实N > 1 时，假设 N - 1 成立，那么对于N成立（N为任意大于1的天然数）。

这里咱们须要分两步。

• ① 假设对于N-1的状况下成立

咱们依然将N-1同时代入等号的左边和右边，得：

1+2+3+...+(n-1) = (n-1)n/2

• ② 将假设结论代入，同时加N

咱们假设N-1是成立的，那么咱们在等号左边与右边同时加N，确定也是成立的,得：

1+2+3...+(n-1)+n = (n-1)n/2+n

化简右边得：n(n+1)/2，那么咱们最后证实的结果就是成立的！

即：1+2+3+...+n = n(n+1)/2 成立。经过以上步骤，咱们能够证实这个公式是成立的。

1.4 小结

概括法适用于想解决一个问题转化为解决他的子问题，而他的子问题又变成子问题的子问题，并且咱们发现这些问题其实都是一个模型，也就是说存在相同的逻辑概括处理项。

接下来咱们来看看，咱们写程序和数学概括法的关联。

2. 递归

提及递归算法，其实咱们每一个开发人员都确定听过或者写过。记得我最开始接触递归算法的时候，仍是大一学习谭浩强老师写的那本C语言时，里面介绍了递归算法。给个人印象就是：本身调用本身。后来在工做中，用到的地方也很少，印象中只有一次写级联菜单的时候用到了递归算法。（是否是我写的代码太水，你们也能够说说哪里用到过递归算法）本章就来经过数学概括法来回顾下咱们曾经学过的递归算法。

2.1 理解递归

递归的基本思想:以此类推

具体来说就是把规模大的问题转化为规模小的类似的子问题来解决。在函数实现时，由于解决大问题的方法和解决小问题的方法每每是同一个方法，因此就产生了函数调用它自身的状况。另外这个解决问题的函数必须有明显的结束条件，这样就不会产生无限递归的状况了。仔细观察递归，就会发现：递归的数学模型其实就是概括法。

2.2 递归条件

咱们在使用递归的时候须要知足一些基本条件，若是不知足的话，就有可能出现无限递归，最后会致使堆栈溢出了。

知足条件：

1. 严格定义递归函数做用，包括参数，返回值，其余变量。
2. 先通常状况，后特殊状况。
3. 有退出条件。在通常状况下，能让递归正常退出的条件。
4. 每次调用必须缩小问题规模，且新问题与原问题有着相同的形式，即规律。

上面的条件一环扣一环，也能够缩减成两个主要条件：有规律,有退出条件。咱们以上面的条件，来结合案例进行理解。

2.3 小栗子

2.3.1 递归求和

例题：

1+2+3+...+n=?

第一步： 严格定义递归函数做用，包括参数，返回值，其余变量。

咱们初看题目，能够知道这是一个简单的求和，即从1开始：1+2+3+...一直加到n。因此咱们能够定义一个入参为n,返回值类型为int的一个方法，既然是递归求和，咱们的方法名就叫recursionSum。

public static int recursionSum(int n) { //为了方便调用，我用了static
    
    return 0;
}

System.out.println("公众号：Coder编程：" + recursionSum(0));

那么咱们第一步就作完了。

第二步： 先通常状况，后特殊状况。

咱们先用通常的状况进行求和计算，例如代入1,2,3这样的通常状况。即：

public static int recursionSum(int n) { 
    if(n == 1) {
        return 1;
    }
    
    if(n == 2) {
        return 1+2;
    }
    
    if(n == 3) {
        return 1+2+3;
    }
    return 0;
}

System.out.println("公众号：Coder编程：" + recursionSum(3));

第三步： 有退出条件。在通常状况下，能让递归正常退出的条件。

其实，咱们作完第二步，就会发现已经把第三步作完了。即有了让递归正常退出的条件！

第四步： 每次调用必须缩小问题规模，且新问题与原问题有着相同的形式，即规律。

这一步是最关键的，也是最核心的！咱们须要找到其规律，而且能缩小问题的规模。咱们会发现，当咱们须要求第N个数的和的时候，咱们必须知道前N-1个数的和，即 sum(N-1)。前N个数的和就是sum(N-1)+N。找到这个规律后，咱们就能够定义一个临时变量sum来接收前N个数的和了。

public static int recursionSum(int n) {

    if(n == 1) {
        return 1;
    }
    
    if(n == 2) {
        return 1+2;
    }
    
    if(n == 3) {
        return 1+2+3;
    }
    
    int sum = recursionSum(n-1)+n;
    return sum;
}

System.out.println("公众号：Coder编程：前5个数的和" + recursionSum(5));

输出结果：15

咱们优化一下：

public static int recursionSum(int n) {

    if (n < 0){
       throw new Exception("参数不能为负！");
    }
    if(n == 1) {
        return 1;
    }
    
    return recursionSum(n-1)+n;
}

System.out.println("公众号：Coder编程：前5个数的和" + recursionSum(5));

是否是忽然发现递归其实也没想的那么难？

2.3.2 触类旁通？

接下来咱们难度进行升级！看你们能不能都理解了。我就不像上面求和那么啰嗦了！

2.3.2.1 求阶乘

例题：求n的阶乘（n>1，n是正整数）

阶乘的递推公式为：factorial(n)=n*factorial(n-1)，其中n为非负整数,且0!=1,1!=1
这里就不作过多说明，跟求后过程一致，能够模仿求和的过程，你们能够先本身尝试写下，下面我直接贴代码了：

public static int factorial(int n) throws Exception {
    if (n < 0){
        throw new Exception("参数不能为负！");
    }else if (n == 1 || n == 0) {
        return 1;
    }else {
        return n * factorial(n - 1);
    }
}

System.out.println("公众号：Coder编程：3的阶乘:" + factorial(3));

输出结果： 公众号：Coder编程：3的阶乘:6

2.3.2.2 斐波那契数列

斐波那契数列 我想你们一样熟悉了解，下面咱们继续回顾一下斐波那契数列究竟是什么？

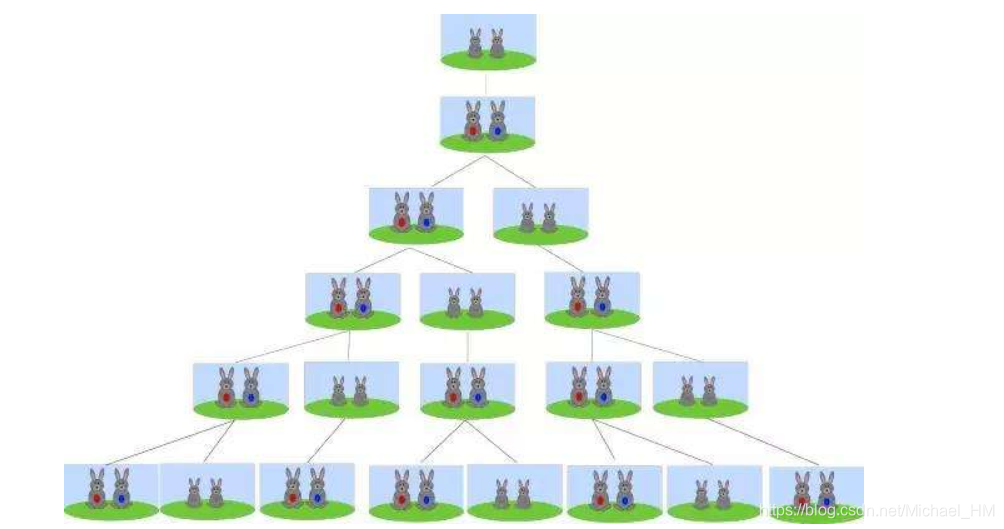
斐波那契数列: 一、一、二、三、五、八、1三、21.....

能够看出从第三位起：第三项等于前两项之和。总结递推公式：:Fib(n)=Fib(n-1)+Fib(n-2)。因此咱们能够将前两位做为退出递归的条件。即：if(n==1) retrun 1 if(n==2) return 1

所以咱们能够直接用公式（规律）和退出条件，写出编程代码：

public static int fib(int n) throws Exception {
    if (n < 0) {
        throw new Exception("参数不能为负！");
    }else if (n == 0 || n == 1){
        return n;
    }else {
        return fib(n - 1) + fib(n - 2);
    }
}

System.out.println("公众号：Coder编程：斐波那契数列:" + fib(3));

2.3.2.3 汉诺塔问题

相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置不一样个数的金盘(以下图)。

游戏的目标：把A杆上的金盘所有移到C杆上，并仍保持原有顺序叠好。

操做规则：每次只能移动一个盘子，而且在移动过程当中三根杆上都始终保持大盘在下，小盘在上，操做过程当中盘子能够置于A、B、C任一杆上。

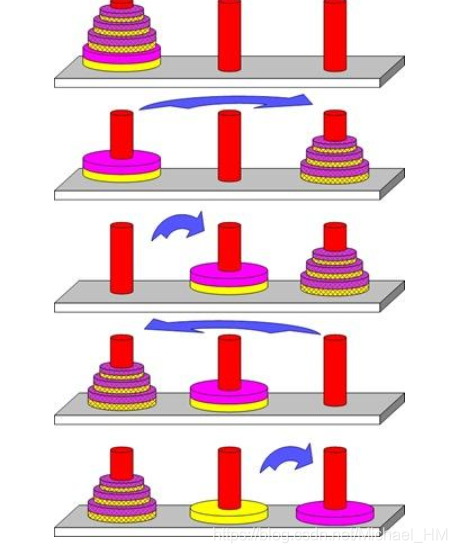
在总结规律和写代码以前，咱们先来玩几把简单的（先通常后特殊）：

注：咱们以数字的大小做为盘子的大小。

1. 一个盘子的状况：

   1.1 将A柱子的1号盘子直接移动到C柱子中。
   1.2 结束。

2. 两个盘子的状况：

   2.1 将A柱子的1号盘子移动到B柱子。
   2.2 将A柱子的2号盘子移动到C柱子。
   2.3 将B柱子的1号盘子移动到C柱子。
   2.4 结束。

3. 三个盘子的状况：

   3.1 将A柱子的1号盘子移动到C柱子。
   3.2 将A柱子的2号盘子移动到B柱子。
   3.3 将C柱子的1号盘子移动到B柱子。
   3.4 将A柱子的3号盘子移动到C柱子。
   3.5 将B柱子的1号盘子移动到A柱子。
   3.6 将B柱子的2号盘子移动到C柱子。
   3.7 将A柱子的1号盘子移动到C柱子。
   3.8 结束。

---

咱们会发现，随着盘子数量的增长，盘子移动的难度也开始加大。

这时候不要惧怕，咱们回过头再来看这个问题：当盘子的数量是4个、5个...N个的时候，咱们该如何解决呢？咱们是否是能够用数学概括法的思想或者递归的思想去解决呢？答案是：确定的。这时候咱们须要去找到他们的规律在哪？

咱们再观察下上面在通常状况下移动盘子的规律在哪？

• 1.当只有一个盘子的时候，能够将盘子直接移动到目标柱子C中。即退出条件。
• 2.当只有两个盘子的时候，咱们只须要将B柱子做为中介，将盘子1先放到中介柱子B上，而后将盘子2放到目标柱子C上，最后将中介柱子B上的盘子放到目标柱子C上便可。

第二点能够当作：当咱们有N个盘子的时候，第N个盘子当作一个盘子，(N-1)个盘子看作成一个盘子。须要将(N-1)个盘子放在中介柱子B上，N个盘子放在目标柱子C便可。即规律。

当咱们有三个盘子的时候，咱们会发现一个问题： 角色变化

1. 将A塔座的第(N-1)~1个盘子当作是一个盘子，放到中柱子B上，而后将第N个盘子放到目标柱子C上。这时候柱子A空了!柱子A成为中介柱子，柱子B成为起始柱子。
2. 柱子B这时候有N-1个盘子，将第(N-2)~1个盘子当作是一个盘子，放到中介柱子A上，而后将柱子B的第(N-1)号盘子放到目标柱子C上。这时候柱子B空了!柱子B又成为了中介柱子，A成为了起始柱子!

重复一、2步骤，直到全部盘子都放到目标塔座C上结束。

总结一下：

1. 从初始柱子A上移动包含n-1个盘子到中介柱子B上。
2. 将初始柱子A上剩余的一个盘子（最大的一个盘子）放到目标柱子C上。
3. 将中介柱子B上n-1个盘子移动到目标柱子C上。

move(3,"A","B","C");

/**
 * 汉诺塔问题
 * @param dish 盘子个数(也表示名称)
 * @param from 初始柱子
 * @param temp 中介柱子
 * @param to   目标柱子
 */
public static void move(int dish,String from,String temp,String to){
    if(dish == 1){
        System.out.println("将盘子"+dish+"从柱子"+from+"移动到目标柱子"+to);
    }else{
        move(dish-1,from,to,temp);//A为初始柱子，B为目标柱子，C为中介柱子
        System.out.println("将盘子"+dish+"从柱子"+from+"移动到目标柱子"+to);
        move(dish-1,temp,from,to);//B为初始柱子，C为目标柱子，A为中介柱子
    }
}

• move(dish-1,from,to,temp);//A为初始柱子，B为目标柱子，C为中介柱子

这里须要将n-1以前的盘子都放到B柱子上，最后第n个盘子放到C柱子。

• move(dish-1,temp,from,to);//B为初始柱子，C为目标柱子，A为中介柱子

这时候B变为了初始柱子，A成为了目标柱子。将以前n-1个盘子放到C目标柱子中。

打印结果：

文末

本章节主要简单介绍了数学概括法与递归算法的一些思想。但愿对你们有所帮助！
从此我会在每张文章开头增长 每章一点正能量 ，文末增长5个编程相关的英语单词 学点英语。但愿你们和我同样天天都能积极向上，一块儿学习一同进步！

学点英语

• JRE Java Runtime Environment（Java运行环境），运行 JAVA程序所必须的环境的集合，包含JVM标准实现及Java核心类库。
• JSDK Java Software Development Kit，和JDK以及J2SE 等同。
• JDK Java Development Kit(Java开发工具包):包括运行环境 、编译工具及其它工具、源代码等，基本上和J2SE等同。
• J2ME Java 2 Micro Edition（JAVA2精简版）API规格基 于J2SE ，可是被修改成能够适合某种产品的单一要求。J2ME使JAVA程序能够很方便的应用于电话卡、寻呼机等小型设备，它包括两种类型的组件，即配置 （configuration）和描述（profile）。

欢迎关注公众号： Coder编程
获取最新原创技术文章和相关免费学习资料，随时随地学习技术知识！

参考文章：

https://www.cnblogs.com/ysoce...

http://www.nowamagic.net/libr...

推荐阅读

一篇带你读懂TCP之“滑动窗口”协议

带你了解数据库中JOIN的用法

深刻浅出了解“装箱与拆箱”